清华大学提出Faster-GCG方法：高效的针对对齐大型语言模型的离散优化监狱突破攻击

动机

在现代人工智能领域，尤其是在大型语言模型（LLMs）中，模型的对齐训练一直是一个重要话题。对齐的LLMs旨在遵循人类的道德标准，并拒绝生成有害或有毒的内容。这些模型在处理各种任务中表现出色，然而，研究发现它们对jailbreak攻击依然脆弱。Jailbreak攻击通常通过特定的提示操纵模型，以引导其生成应该被避免的有害内容，从而揭示了LLMs在安全性方面的固有弱点。这一现象引发了对如何识别和修复LLMs安全漏洞的广泛关注，以防止其被不当使用。

在已有的研究中，Zou等人提出了一种名为GCG（Greedy Coordinate Gradient）的攻击方法，将jailbreak问题形式化为离散的Token优化问题，通过迭代过程寻找能够突破LLMs防御的后缀。然而，该方法在计算效率和攻击效果上表现不佳，导致在较大的计算成本下成功率有限。因此，本文的研究动机在于改进GCG方法，提出一种更高效的新方法——Faster-GCG，旨在以更低的计算成本取得更好的攻击成功率。

本研究的创新点体现在以下几个方面：

  1. 瓶颈识别：通过深入分析GCG方法，识别出其在离散优化过程中的多个瓶颈，指出原有方法在梯度信息利用和Token间距假设等方面的缺陷。
  2. 技术改进：提出了三种简单有效的技术以提高jailbreak攻击的效率，这包括引入与Token间距离相关的正则化项、采用贪婪采样替代随机采样，以及通过历史记录避免自循环问题。
  3. 实验证明：对多种开放源代码的对齐LLMs进行实验证明，Faster-GCG在计算成本减少至原来1/10的情况下显著提高了攻击成功率，这一方法在封闭源LLMs如ChatGPT中的迁移能力也得到了验证。

通过这些创新，本研究为了解和改善LLMs的安全性提供了前景广阔的视角，并为未来的研究提供了重要基础。

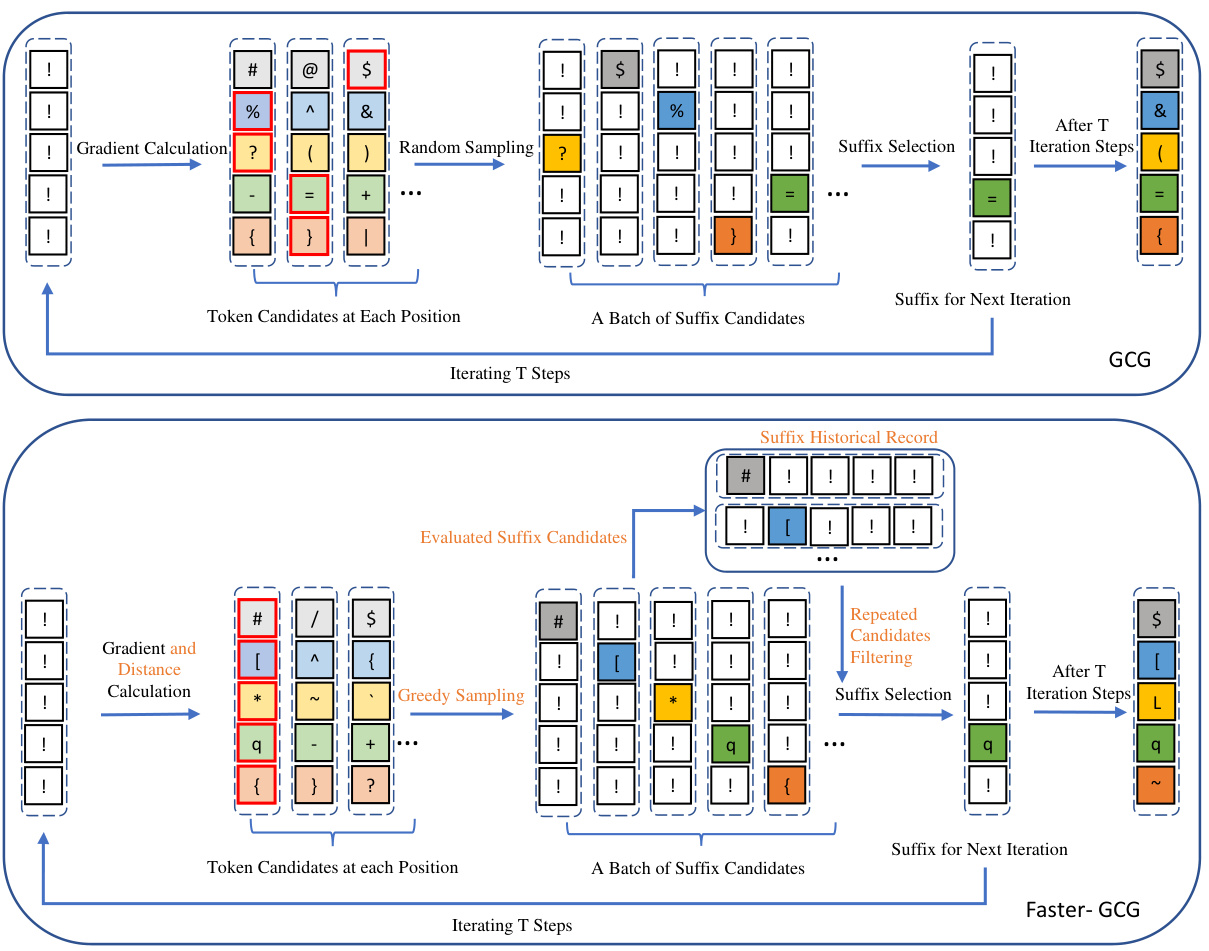
Figure

方法

在本节中，研究者们提出了一种高效的离散优化方法，称为Faster-GCG，以提高对大语言模型（LLMs）进行越狱攻击的效率。Faster-GCG基于GCG方法，首先对越狱问题进行了形式化，然后详细介绍了GCG的工作原理，并讨论了GCG的关键局限性，最后引入了Faster-GCG中的改进技术。

越狱问题的形式化

设定输入为由分词器生成的Token序列。令xk∈{1,2,…,m}x_k \in \{1, 2, \ldots, m\}表示词汇表中单个Token，x\mathbf{x}或x1:l\mathbf{x}_{1:l}表示长度为ll的Token序列。LLM被视为从Token序列x1:l\mathbf{x}_{1:l}映射到下一个Token的概率分布，即:

pθ(xl+1∣emb(x1:l)),p_{\theta}(x_{l+1} \mid \text{emb}(\mathbf{x}_{1:l})),

其中pθ(⋅)p_{\theta}(\cdot)表示LLM的输出概率，emb(⋅)\text{emb}(\cdot)表示将每个Token映射为维度为dd的向量的嵌入函数。为简便起见，在大多数情况下省略emb(⋅)\text{emb}(\cdot)。

如下图所示，越狱任务可以形式化为一个离散优化问题。给定系统提示\mathbfcal{X}^{(s_1)}、用户请求\mathbfcal{X}^{(u)}和连接系统提示\mathbfcal{X}^{(s_2)}，目标是找到一个固定长度为nn的对抗后缀\mathbfcal{X}^{(a)}，使得交叉熵损失L(x(a))\mathcal{L}(\mathbf{x}^{(a)})最小化，在此损失中，LLM的输出与预定义的优化目标x(t)\mathbf{x}^{(t)}（有害内容）之间进行比较。

\begin{align*} \mathcal{L}(\mathbf{x}^{(a)}) = -\log p_{\theta}(\mathbf{x}^{(t)} \mid \mathbf{x}^{(s_1)} \oplus \mathbf{x}^{(u)} \oplus \mathbf{x}^{(a)} \oplus \mathbf{x}^{(s_2)}) \end{align*}

该过程将优化目标转化为寻找最小化该损失的对抗后缀的问题。

GCG的初步介绍

GCG通过以下两步迭代过程寻求最小化上述目标来找到越狱后缀：

  1. 候选选择：GCG首先选择一组有前景的Token在后缀的每个位置进行替换，这通过计算损失函数L\mathcal{L}对一热编码Token指示矩阵的梯度来实现：

    G=∂L∂E∈Rm×n.G = \frac{\partial \mathcal{L}}{\partial \mathbf{E}} \in \mathbb{R}^{m \times n}.

    对于后缀的每个Token位置ii，GCG识别最可能降低损失的候选Token Xi\mathcal{X}_{i}，依赖于梯度信息：

    Xi:=Top−K(−gi).\mathcal{X}_{i} := \text{Top}-K(-\mathbf{g}_{i}).

  2. 精确评估替换：在获得Xi\mathcal{X}_{i}后，GCG生成后缀候选x~1:n(b)\tilde{x}_{1:n}^{(b)}，通过复制当前后缀并从前K个替换中随机选择一个替换Tokenx~i(b)\tilde{x}_{i}^{(b)}，计算每个候选的精确损失，并选择具有最低损失的替换Token，用于下一次迭代。

GCG的关键限制

研究者发现GCG在计算开销和越狱性能上存在显著的高成本，且效果有限。分析显示关键限制包括：

  • 近似误差依赖于不切实际的假设。
  • 从前K梯度中随机采样导致低效的优化。
  • 自环问题使得算法在迭代中可能返回到之前的状态，导致效率降低。

Faster-GCG

为了解决上述限制，Faster-GCG引入了三种简单但有效的技术：

  • 附加正则化项：在候选Token选择过程中引入与Token间距相关的正则化项，通过权重g^k\hat{g}_{k}改进梯度估计，以提高Token选择的准确性：

    g^k=∂L∂ek+w⋅∥Xj−Xk∥.\hat{g}_{k} = \frac{\partial \mathcal{L}}{\partial e_{k}} + w \cdot \|X_{j} - X_{k}\|.

  • 贪婪采样：用确定性贪婪采样替代随机采样，按g^\hat{g}的值从高到低顺序选择，进一步加快搜索的收敛速度。

  • 避免自环问题：保持已评估后缀的历史记录，过滤掉重复的状态，从而防止迭代中的自环。

通过这些改进，Faster-GCG有效提高了越狱攻击的性能。本节的伪代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Require: 初始后缀 $x_{1:n}$，迭代次数 $T$，损失函数 $\mathcal{L} := \mathcal{L}_{CW}$，批量大小 $B$，历史记录集 $\mathcal{S} := \emptyset$

loop $T$ 次
    for $i=1$ to $n$ do
        计算正则化梯度 $-\hat{g}^{(i)}$ 
        $b=0$ 
        while $b<B$ do
            $\tilde{x}_{1:n}^{(b)} := x_{1:n}$
            更新 $\tilde{x}_{i}^{(b)}$ 采用贪婪采样
            if $\tilde{x}_{1:n}^{(b)} \notin \mathcal{S}$ then
                计算损失 $\mathcal{L}(\tilde{x}_{1:n}^{(b)})$
                $S = S \cup \{ \tilde{x}_{1:n}^{(b)} \}$ 
                $b = b + 1$
        $x_{1:n} := \tilde{x}_{1:n}^{(b^{*})}$，其中 $b^{*}=\arg\min_{b} \mathcal{L}(\tilde{x}_{1:n}^{(b)})$
        
return 优化后的后缀 $x_{1:n}$

通过这些策略，Faster-GCG能够在效率和效果上都取得提升，有效地挖掘LLMs的脆弱性。

实验

在本研究中，Faster-GCG方法的有效性通过一系列实验进行了验证，实验包括开放源代码与封闭源代码的大型语言模型（LLMs）的针对性攻击。

实验设置

模型方面，研究团队测试了Faster-GCG在四个大型语言模型上的表现，包括两个开放源代码模型：Vicuna-13B和Llama-2-7B-chat，以及两个封闭源代码模型：GPT-3.5-Turbo和GPT-4。实验使用了JBB-Behaviors数据集，该数据集包含100个精心设计的行为场景，用于评估对大型语言模型的攻击成功率（ASR）。

白盒设置下的结果

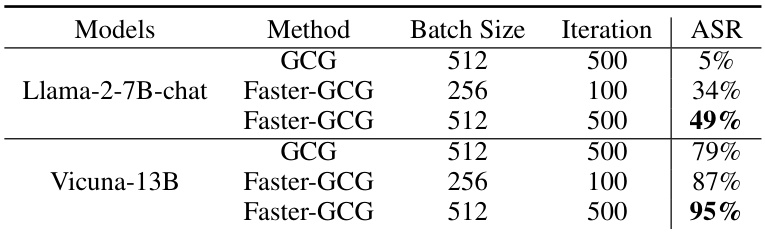
在白盒设置中，Faster-GCG的大幅改进在于，无论是在计算成本上还是在攻击成功率上都显著超越了原始的GCG方法。具体而言，在Llama-2-7B-chat模型上，Faster-GCG的ASR提高了31%，而对于Vicuna-13B模型，ASR的提升为7%。为了进一步验证效果，实验还展示了Faster-GCG在相同计算成本下明显更高的攻击成功率。

以下是Llama-2-7B-chat和Vicuna-13B在JBB-Behaviors数据集上的结果（表格省略）：

黑盒设置下的结果

Faster-GCG还展示了出色的转移能力。当Vicuna-13B模型生成的后缀被直接应用于封闭源代码模型时，Faster-GCG生成的后缀在封闭源代码模型中的表现优于GCG。这一结果表明，Faster-GCG所生成的后缀具有更好的通用性。

以下是封闭源代码LLMs在黑盒设置下的结果（表格省略）：

消融研究

为了更深入地了解Faster-GCG的改进效果，研究人员开展了消融研究，分别禁用不同的技术，以评估每种技术对ASR的影响。结果显示，距离正则化项的去除导致ASR下降14%，而消除自环预防措施带来了20%的ASR降幅，显示出避免冗余循环对有效优化的重要性。

以下是Llama-2-7B-chat模型的消融研究结果（表格省略）：

损失对比

在实验过程中，Faster-GCG和GCG的损失值曲线也进行了比较。Faster-GCG的损失值在整个迭代过程中始终低于GCG，表明其在离散优化效率上的提升。

以下是GCG与Faster-GCG的损失曲线对比图（见图3）：

Average loss comparison between GCG and Faster-GCG

通过这些实验，Faster-GCG在多个方面的有效性和效率得到了验证，展现了其作为一种竞争性方法的潜力。

结论

本文提出了Faster-GCG，一种优化且高效的对抗性越狱方法，针对大型语言模型（LLMs）。通过识别并解决原始GCG方法中的关键瓶颈，Faster-GCG在攻击成功率方面实现了显著提升，同时将计算成本降低了十倍。实验结果表明，Faster-GCG不仅在像Llama-2-7B-chat和Vicuna-13B等开源LLMs上超越了GCG，而且在应用于闭源模型时也表现出更好的转移能力。这些结果表明，尽管在使LLMs更好地遵循预期行为的努力中取得了进展，但对抗性越狱攻击仍然是一个关键的安全漏洞。Faster-GCG的卓越表现强调了需要持续改善LLMs的对齐能力，以应对这些风险。

尽管如此，本文也指出了一些局限性。例如，与GCG相似，Faster-GCG优化的对抗性后缀在困惑度方面要高于自然语言，这使得通过基于困惑度的检测机制易于识别。此外，Faster-GCG没有在转移基础攻击设置中采用集成技术，这通常会显著提升黑盒攻击的攻击成功率。作者计划在未来的工作中继续致力于解决这些问题。

最后，作者认为Faster-GCG可以作为基础的离散优化算法，适用于超越LLMs的多种模型，如文本到图像的扩散模型。这将有助于在不同领域中推动AI安全的更广泛理解和协作发展。